Teorema del coseno
El teorema del coseno es una generalización del teorema de Pitágoras en los triángulos rectángulos que se utiliza, normalmente, en trigonometría.
El teorema relaciona un lado de un triángulo cualquiera con los otros dos y con el coseno del ángulo formado por estos dos lados:
|
En la mayoría de los idiomas, este teorema es conocido con el nombre de teorema del coseno, denominación no obstante relativamente tardía. En francés, sin embargo, lleva el nombre del matemático persa Ghiyath al-Kashi que unificó los resultados de sus predecesores.1
Índice
[ocultar]Historia[editar]
Los Elementos de Euclides, que datan del siglo III a. C., contienen ya una aproximación geométrica de la generalización delteorema de Pitágoras: las proposiciones 12 y 13 del libro II, tratan separadamente el caso de un triángulo obtusángulo y el de un triángulo acutángulo. La formulación de la época es arcaica ya que la ausencia de funciones trigonométricas y delálgebra obligó a razonar en términos de diferencias de áreas.2 Por eso, la proposición 12 utiliza estos términos:
«En los triángulos obtusángulos, el cuadrado del lado opuesto al ángulo obtuso es mayor que los cuadrados de los lados que comprenden el ángulo obtuso en dos veces el rectángulo comprendido por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso».Euclides, Elementos.3
Siendo ABC el triángulo, cuyo ángulo obtuso está en C, y BH la altura respecto del vértice B (cf. Fig. 2 contigua), la notación moderna permite formular el enunciado así:
Faltaba esperar la trigonometría árabe-musulmana de la Edad Media para ver al teorema evolucionar a su forma y en su alcance: el astrónomo y matemático al-Battani4 generalizó el resultado de Euclides en la geometría esférica a principios delsiglo X, lo que permitió efectuar los cálculos de la distancia angular entre el Sol y laTierra.5 6 Fue durante el mismo período cuando se establecieron las primeras tablas trigonométricas, para las funciones seno y coseno. Eso permitió a Ghiyath al-Kashi,7 matemático de la escuela de Samarcanda, de poner el teorema bajo una forma utilizable para la triangulación durante el siglo XV. La propiedad fue popularizada en occidente por François Viètequien, al parecer, lo redescubrió independientemente.8
Fue a finales del siglo XVII cuando la notación algebraica moderna, aunada a la notación moderna de las funciones trigonométricas introducida por Euler en su libro Introductio in analysin infinitorum, permitieron escribir el teorema bajo su forma actual, extendiéndose el nombre de teorema (o ley) del coseno.9
El teorema y sus aplicaciones[editar]
El teorema del coseno es también conocido por el nombre de teorema de Pitágoras generalizado, ya que el teorema de Pitágoras es un caso particular: cuando el ángulo  es recto o, dicho de otro modo, cuando
es recto o, dicho de otro modo, cuando 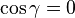 , el teorema del coseno se reduce a:
, el teorema del coseno se reduce a:
 es recto o, dicho de otro modo, cuando
es recto o, dicho de otro modo, cuando 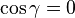 , el teorema del coseno se reduce a:
, el teorema del coseno se reduce a:
que es precisamente la formulación del teorema de Pitágoras.
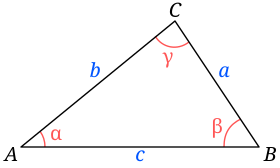
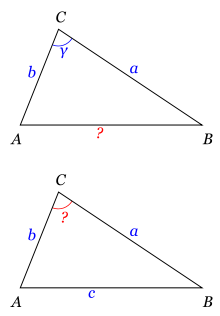
El teorema se utiliza en triangulación (ver Fig. 3) para resolver un triángulo, y saber determinar:
- el tercer lado de un triángulo cuando conocemos un ángulo y los lados adyacentes:
.
- los ángulos de un triángulo cuando conocemos los tres lados:
.
Estas fórmulas son difíciles de aplicar en el caso de mediciones de triángulos muy agudos utilizando métodos simples, es decir, cuando el lado c es muy pequeño respecto los lados a y b —o su equivalente, cuando el ángulo γ es muy pequeño.
Existe un corolario del teorema del coseno para el caso de dos triángulos semejantes ABC y A'B'C'
.
Demostraciones[editar]
Por desglose de áreas[editar]
Un cierto número de las demostraciones del teorema hacen intervenir un cálculo de áreas. Conviene en efecto remarcar que
- a2, b2, c2 son las áreas de los cuadrados de lados respectivos a, b, c.
- ab cos(γ) es el área de un paralelogramo de lados a y b que forman un ángulo de 90°-γ (para una prueba, ver el apéndice).
Dado que cos(γ) cambia de signo dependiendo de si γ es mayor o menor a 90°, se hace necesario dividir la prueba en dos casos.
La figura 4a (contigua) divide un heptágono de dos maneras diferentes para demostrar el teorema del coseno en el caso de un ángulo agudo. La división es la siguiente:
- En verde, las áreas a2, b2 la izquierda, y el área , c2 a la derecha.
- En rojo, el triángulo ABC en ambos diagramas y en amarillo triángulos congruentes al ABC.
- En azul, paralelogramos de lados a y b con ángulo 90°-γ.
Igualando las áreas y cancelando las figuras iguales se obtiene que  , equivalente al Teorema del coseno.
, equivalente al Teorema del coseno.
 , equivalente al Teorema del coseno.
, equivalente al Teorema del coseno.
La figura 4b (contigua) desglosa un hexágono de dos maneras diferentes para demostrar el teorema del coseno en el caso de un ángulo obtuso. La figura muestra
- En verde a2, b2 la izquierda y c2 a la derecha.
- En azul -2ab cos(γ), recordando que al ser cos(γ) negativo, la expresión completa es positiva.
- En rojo, dos veces el triángulo ABC para ambos lados de la figura.
Igualando áreas y cancelando las zonas rojas da  , como queríamos demostrar.
, como queríamos demostrar.
 , como queríamos demostrar.
, como queríamos demostrar.Por el teorema de Pitágoras[editar]
Notemos que el Teorema de Cosenos es equivalente al Teorema de Pitágoras cuando el ángulo  es recto. Por tanto sólo es necesario considerar los casos cuando c es adyacente a dos ángulos agudos y cuando c es adyacente a un ángulo agudo y un obtuso.
es recto. Por tanto sólo es necesario considerar los casos cuando c es adyacente a dos ángulos agudos y cuando c es adyacente a un ángulo agudo y un obtuso.
 es recto. Por tanto sólo es necesario considerar los casos cuando c es adyacente a dos ángulos agudos y cuando c es adyacente a un ángulo agudo y un obtuso.
es recto. Por tanto sólo es necesario considerar los casos cuando c es adyacente a dos ángulos agudos y cuando c es adyacente a un ángulo agudo y un obtuso.
Primer caso: c es adyacente a dos ángulos agudos.
Consideremos la figura adjunta. Por el teorema de Pitágoras, la longitud c es calculada así:
(left)
Pero, la longitud h también se calcula así:
(left)
Sumando ambas ecuaciones y luego simplificando obtenemos:
Por la definición de coseno, se tiene:
y por lo tanto:
Sustituimos el valor de u en la ecuación para c2, concluyendo que:
con lo que concluye la prueba del primer caso.
Segundo caso: c es adyacente a un ángulo obtuso.
Consideremos la figura adjunta. El teorema de Pitágoras establece nuevamente  pero en este caso
pero en este caso  . Combinando ambas ecuaciones obtenemos
. Combinando ambas ecuaciones obtenemos  y de este modo:
y de este modo:
 pero en este caso
pero en este caso  . Combinando ambas ecuaciones obtenemos
. Combinando ambas ecuaciones obtenemos  y de este modo:
y de este modo:.
De la definición de coseno, se tiene  y por tanto:
y por tanto:
 y por tanto:
y por tanto:.
Sustituimos en la expresión para  , concluyendo nuevamente
, concluyendo nuevamente
 , concluyendo nuevamente
, concluyendo nuevamente.
Esto concluye la demostración. c2 = a2 - b2 - 2b(a cos(γ) - b) Es importante notar, que si se considera a u como unsegmento dirigido, entonces sólo hay un caso y las dos demostraciones se convierten en la misma.
Por la potencia de un punto con respecto a un círculo[editar]
Consideremos un círculo con centro en B y radio BC, como en la figura 6. Si AC es tangente al círculo, nuevamente se tiene el Teorema de Pitágoras. Cuando AC no es tangente, existe otro punto K de corte con el círculo. LA potencia del punto A con respecto a dicho círculo es
.
Por otro lado, AL = c+a y AP = c-a de modo que
.
Además, CK= -2a cos(γ) (ver el apéndice) por lo que
.
Igualando las expresiones obtenidas se llega finalmente a:
Contrariamente a las precedentes, para esta demostración, no es necesario recurrir a un estudio por caso pues las relaciones algebraicas son las mismas para el caso del ángulo agudo.
Por el cálculo vectorial[editar]
Utilizando el cálculo vectorial, más precisamente el producto escalar, es posible encontrar el teorema del coseno en algunas líneas:






















No hay comentarios:
Publicar un comentario